1 - Simulación Circuito RC Básico

Fórmulas del Método de Euler

Consideramos una ecuación diferencial ordinaria dada por:

Donde $y(t_0)$ es el valor inicial. La derivada en la ecuación anterior puede aproximarse por:

Substituyendo esta aproximación en la ecuación diferencial y reorganizando los términos para calcular el siguiente valor de $y$, se obtiene:

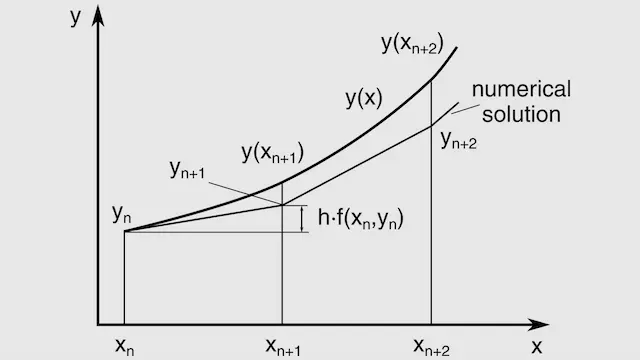
Esta ecuación se puede utilizar iterativamente, avanzando la solución a $t = t_0 + 2\Delta t$ usando $y(t_0 + \Delta t)$, y así sucesivamente. Generalizando para cualquier paso iterativo, tenemos:

Esta es la ecuación iterativa de Euler, que se utiliza frecuentemente en ingeniería debido a su simplicidad y rapidez. Sin embargo, tiene la desventaja de no ser particularmente precisa y solo es condicionalmente estable. El error en el método de Euler es proporcional al tamaño del paso de tiempo $\Delta t$. Reducir $\Delta t$ mejora la precisión de la aproximación.

Aqui tienes un codigo que podria servirte para la implementación:

function [t, y] = eulerMethod(f, t0, y0, dt, tf)
    % f es la función diferencial f(t, y)
    % t0 es el tiempo inicial
    % y0 es el valor inicial de y en t = t0
    % dt es el paso de tiempo \Delta t
    % tf es el tiempo final de la simulación
    
    % Calcula el número de pasos necesarios
    N = floor((tf - t0) / dt);
    
    % Inicializa vectores de tiempo y solución
    t = zeros(1, N+1);
    y = zeros(1, N+1);
    
    % Establece las condiciones iniciales
    t(1) = t0;
    y(1) = y0;
    
    % Itera el método de Euler
    for i = 1:N
        t(i+1) = t(i) + dt;
        y(i+1) = y(i) + f(t(i), y(i)) * dt;
    end
end