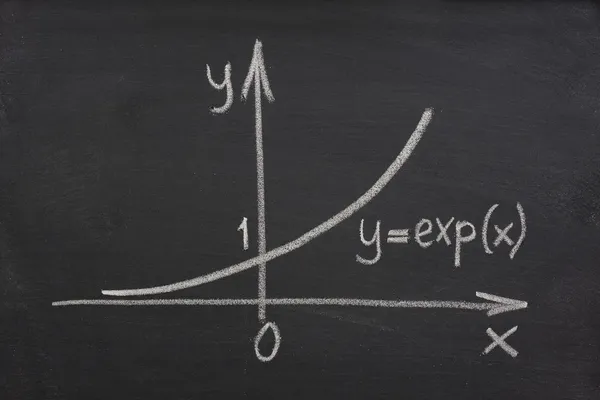
FUNCIÓN EXPONENCIAL

La función exponencial

Tiene una gran importancia para el curso de EDyMN.

Se define como:

Donde:

• $y(t)$: Valor de la función exponencial en el tiempo $t$.
• $e$: Base del logaritmo natural, aproximadamente igual a 2.71828.
• $a$: Constante que determina la tasa de crecimiento o decrecimiento de la función.
• $t$: Variable independiente, usualmente representa el tiempo.

Propiedades:

1. $e^0=1$

2. $e^{at{\,\color{red}+}\,c}=e^{at}{\,\color{red}\cdot}\, e^c$

3. $e^{at}$ nunca es $0$

4. $a>0 \Rightarrow \lim\limits_{t \to {\color{green}\infty} }e^{at}=\infty \;\wedge\; \lim\limits_{t \to {\color{red}-\infty} }e^{at}=0$

5. $a<0 \Rightarrow \lim\limits_{t \to{\color{green}\infty} }e^{at}=0 \;\wedge\; \lim\limits_{t \to {\color{red}-\infty }}e^{at}=\infty$

6. Para cualquier positivo $a, \:e^{at}$ crecerá mucho más rápido que cualquier polinomio, ejemplo:

   $$\lim\limits_{t \to\infty }\cfrac{e^{t}}{t^3}=\infty \;\wedge\; \lim\limits_{t \to \infty }te^{-t}=0$$

Representación gráfica