S. Chavez 🛸
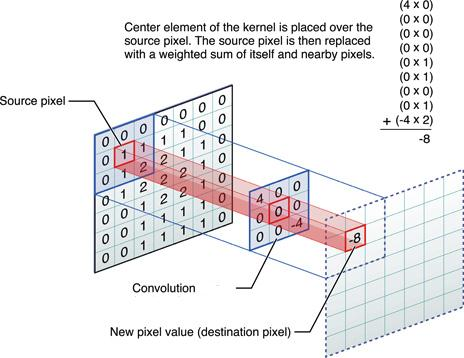
CONVOLUCIÓN Y FUNCIÓN ESCALÓN UNITARIO

CONVOLUCIÓN Y FUNCIÓN ESCALÓN UNITARIO


Apunte
EDO Laplace Convolución Escalón

Convolución en transformada de Laplace

Convolución:

f(x)∗g(x)=∫0xf(t) g(x−t)dtf(x)*g(x)=\int_0^x f(t)~g(x-t)dt

Convolución para t. de Laplace:

L[ f(x) g(x) ]=No existe formula\mathscr{L}[~f(x)~g(x)~]=\text{No existe formula} L−1[ F(s) G(s) ]=∫0xf(t) g(x−t)dt=f(x)∗g(x)\mathscr{L}^{-1}[~F(s)~G(s)~]=\int_0^x f(t)~g(x-t)dt =f(x)*g(x)

Teorema de la convolución:

L[ f(x)∗g(x) ]=L[f(x)] L[g(x)]=F(s) G(s)\mathscr{L}[~f(x)*g(x)~]=\mathscr{L}[f(x)]~\mathscr{L}[g(x)]=F(s)~G(s)

Función escalón unitario

También conocida como función de Heaviside

u(x)={0x<01x≥0u(x)=\left\lbrace \begin{align*} 0 \qquad&x<0 \\ 1 \qquad&x\geq0 \end{align*}\right.

Entonces:

u(x−c)={0x<c1x≥cu(x-c)=\left\lbrace \begin{align*} 0 \qquad&x<c \\ 1 \qquad&x\geq c \end{align*}\right.

Teorema:

L[u(x−c)]=1se−cs\mathscr{L}[u(x-c)]=\frac{1}{s}e^{-cs}

Traslaciones

u(x−c) f(x−c)={0      x<cf(x−c)x≥cu(x-c)~f(x-c)=\left\lbrace \begin{align*} 0~~~~~~ \qquad&x<c \\ f(x-c) \qquad&x\geq c \end{align*}\right.

Traslación o desplazamiento de la función f(x)f(x) por cc unidades en la dirección xx positiva

Teorema:

L[ u(x−c) f(x−c) ]=e−csF(s)∣F(s)=L[ f(x) ]\mathscr{L}[~u(x-c)~f(x-c)~]=e^{-cs}F(s) \qquad\qquad|\qquad\qquad F(s)=\mathscr{L}[~f(x)~]

Para la inversa:

L−1[ e−csF(s) ]=u(x−c) f(x−c)={0      x<cf(x−c)x≥c\mathscr{L}^{-1}[~e^{-cs}F(s)~]= u(x-c)~f(x-c)= \left\lbrace \begin{align*} 0~~~~~~ \qquad&x<c \\ f(x-c) \qquad&x\geq c \end{align*}\right.

Ejercicios

  1. Calcular:

    L[et∗t2]\mathscr{L}[ e^t*t^2]

    Utilice convolución, luego el teorema

Solución 🎁

  • Para la convolución

    et∗t2=t2∗et=∫0t(x2)(et−x) dx=∫0tx2ete−x dx=et∫0te−xx2 dx\begin{align*} e^t*t^2 &=t^2*e^t\\ &=\int_0^t (x^2)(e^{t-x}) \, dx\\ &=\int_0^t x^2 e^t e^{-x} \, dx\\ &=e^t \int_0^t e^{-x} x^2 \, dx \end{align*}

  • integrando por partes

    ∫u dv=uv−∫v du\int u \, dv=u v-\int v \, du ∫e−xx2 dx=(x2)(−e−x)−∫(−e−x)(2x dx)\int e^{-x} x^2 \, dx= (x^2)(-e^{-x})-\int (-e^{-x})(2x~dx)
x2(−et−x)∣0t+(2et)∫0te−xx dxx^2 \left(-e^{t-x}\right)\Big|_{0}^t+\left(2 e^t\right) \int_0^t e^{-x} x \, dx
x2(−et−x)∣0t=(−et−tt2)−(02(−et−0))=−t2x^2 \left(-e^{t-x}\right)\Big|_{0}^t=(-e^{t-t}t^2)-(0^2(-e^{t-0}))=-t^2
−t2+(2et)∫0te−xx dx-t^2+\left(2 e^t\right) \int_0^t e^{-x} x \, dx
∫e−x dx=(x)(−e−x)−∫(−e−x)(dx)\int e^{-x} \, dx= (x)(-e^{-x})-\int (-e^{-x})(dx)
−t2+(−2xet−x)∣0t+2et∫0te−x dx-t^2+ (-2 xe^{t-x}) \Big|_{0}^t + 2e^t\int_0^t e^{-x} \, dx
(−2xet−x)∣0t=(−2tet−t)−(−2(0)et−0)=−2t(-2 xe^{t-x}) \Big|_{0}^t =(-2 te^{t-t})-(-2(0)e^{t-0})=-2t
−t2−2t+2et∫0te−x dx-t^2-2t + 2e^t\int_0^t e^{-x} \, dx
−t2−2t+(2et−x)∣0t-t^2-2t + (2e^{t-x})\Big|_{0}^t
−t2−2t+(2et−2)-t^2-2t + (2e^{t}-2)

  • Laplace

    L[−t2−2t−2+2et]\mathscr{L}[-t^2-2t-2 + 2e^{t}]
−L[t2]−2L[t]−L[2]+2L[et]-\mathscr{L}[t^2]-2\mathscr{L}[t]-\mathscr{L}[2] + 2\mathscr{L}[e^{t}]
−2s3−2s2−2s+2s−1-\frac{2}{s^3}-\frac{2}{s^2}-\frac{2}{s}+\frac{2}{s-1}
−2s3−2s2−2s+2s−1=−2(s−1)−2s(s−1)−2s2(s−1)+2s3s3(s−1)=2s3(s−1)-\frac{2}{s^3}-\frac{2}{s^2}-\frac{2}{s}+\frac{2}{s-1} =\frac{-2(s-1)-2s(s-1)-2s^2(s-1)+2s^3}{s^3(s-1)}=\frac{2}{s^3(s-1)}

  • Por el teorema de la convolución:

    L[et∗t2]=L[et] L[t2]\mathscr{L}[ e^t*t^2]=\mathscr{L}[e^t]~\mathscr{L}[t^2]
L[et] L[t2]=1s−1⋅2s3=2s3(s−1)\mathscr{L}[e^t]~\mathscr{L}[t^2] =\frac{1}{s-1}\cdot \frac{2}{s^3} =\frac{2}{s^3(s-1)}

  1. Encontrar:

    f(x)∗g(x)Cuandof(x)=e3x∧g(x)=e2xf(x)*g(x)\quad\text{Cuando}\quad f(x)=e^{3x} \quad\land\quad g(x)=e^{2x}
Solución 🎁

  • Se tiene que:

    f(t)=e3t∧g(x−t)=e2(x−t)f(t)=e^{3t} \quad\land\quad g(x-t)=e^{2(x-t)}

  • Finalmente:

    e3x−e2xe^{3x}-e^{2x}

  1. Encontrar:

    L−1[ 1s2−5s+6 ]\mathscr{L}^{-1}\left[~\frac{1}{s^2-5s+6}~\right]

    Usar convoluciones

Solución 🎁

  • Se tiene:

    1s2−5s+6=1(s−3)(s−2)=1s−3⋅1s−2\frac{1}{s^2-5s+6}=\frac{1}{(s-3)(s-2)}=\frac{1}{s-3}\cdot\frac{1}{s-2}

  • Entonces:

    L−1[ 1s2−5s+6 ]=f(x)∗g(x)=e3x∗e2x\mathscr{L}^{-1}\left[~\frac{1}{s^2-5s+6}~\right]=f(x)*g(x)=e^{3x}*e^{2x}

  • Finalmente:

    e3x−e2xe^{3x}-e^{2x}

  1. Graficar:

    f(x)=u(x−2)−u(x−3)f(x)=u(x-2)-u(x-3)
Solución 🎁

  • Se tiene:

    u(x−2)={0x<21x≥2u(x-2)= \left\lbrace \begin{align*} 0 \qquad&x<2 \\ 1 \qquad&x\geq 2 \end{align*}\right. u(x−3)={0x<31x≥3u(x-3)= \left\lbrace \begin{align*} 0 \qquad&x<3 \\ 1 \qquad&x\geq 3 \end{align*}\right.

  • Entonces:

    f(x)=u(x−2)−u(x−3)={0−0=0x<21−0=12≥x<31−1=0x≥3f(x)=u(x-2)-u(x-3)= \left\lbrace \begin{align*} 0-0=0 \qquad&x<2 \\ 1-0=1 \qquad&2\geq x<3\\ 1-1=0 \qquad&x\geq 3 \\ \end{align*}\right.

  1. Graficar:

    f(x)=5−5u(x−8)∣x≥0f(x)=5-5u(x-8) \qquad\qquad|\qquad\qquad x\geq0
Solución 🎁

  • Se tiene:

    5u(x−8)={0x<85x≥85u(x-8)= \left\lbrace \begin{align*} 0 \qquad&x<8 \\ 5 \qquad&x\geq 8 \end{align*}\right. 5={5x<85x≥85= \left\lbrace \begin{align*} 5 \qquad&x<8 \\ 5 \qquad&x\geq 8 \end{align*}\right.

  1. Encontrar L[ g(x) ]\mathscr{L}[~g(x)~]:

    g(x)={0       x<4(x−4)2x≥4g(x)= \left\lbrace \begin{align*} 0~~~~~~~ \qquad&x<4 \\ (x-4)^2 \qquad&x\geq 4 \end{align*}\right.
Solución 🎁

  • Se define:

    f(x)=x2f(x)=x^2
g(x)=u(x−4) f(x−4)=u(x−4)(x−4)2g(x)=u(x-4)~f(x-4)=u(x-4)(x-4)^2
L[ f(x) ]=F(s)\mathscr{L}[~f(x)~]=F(s)
L[ f(x) ]=F(s)=2s3\mathscr{L}[~f(x)~]=F(s)=\frac{2}{s^3}
L[ g(x) ]=L[ u(x−4)(x−4)2 ]\mathscr{L}[~g(x)~]=\mathscr{L}[~u(x-4)(x-4)^2 ~]
L[ g(x) ]=L[ u(x−4)(x−4)2 ]=e−4s2s3\mathscr{L}[~g(x)~]=\mathscr{L}[~u(x-4)(x-4)^2 ~]=e^{-4s}\frac{2}{s^3}